Hier ist etwas zum Rechnen, Spielen und Raten

Falls Sie eine Rampe mit gleichmäßigem Gefälle und gleicher Beschaffenheit bergab befahren, möchten Sie vielleicht wissen, welche Geschwindigkeit Sie erreichen können, wenn Sie bei Null starten und die Füße ruhig halten, die Pedale also nicht bewegen. Die Lösung des Problems sind die Formeln aus Teil 1. Falls Sie diese nicht selbst ausrechnen wollen, wofür erfahrensgemäß viel spricht, hilft Ihnen mein Programm. Für die Reibungskoeffizienten habe ich durchschnittliche Werte gesetzt; der Rollwiderstand sei µ = 0.004; der Luftwiderstand κ = 0.35 kg/m. Voraussetzungen: Sie haben den Mut, bergab ohne zu bremsen zu fahren. Wozu ich Sie aber keineswegs ermutigen möchte, denn schnell erreichen Sie bei steiler Abfahrt Geschwindigkeiten, die Sie womöglich nicht mehr kontrollieren können. Außerdem sollte kein zusätzlicher Gegenwind (außer dem von Ihnen selbst verursachten) die Abfahrt behindern. Nach Eingabe von Steigung und Gesamtgewicht erhalten Sie die Antwort auf folgende Frage:
Welche Zeit t_max benötige ich für die Strecke s_max, um eine Geschwindigkeit v_max zu erreichen, die sich um weniger als 1 Promille von der theoretisch erreichbaren Geschwindigkeit unterscheidet.

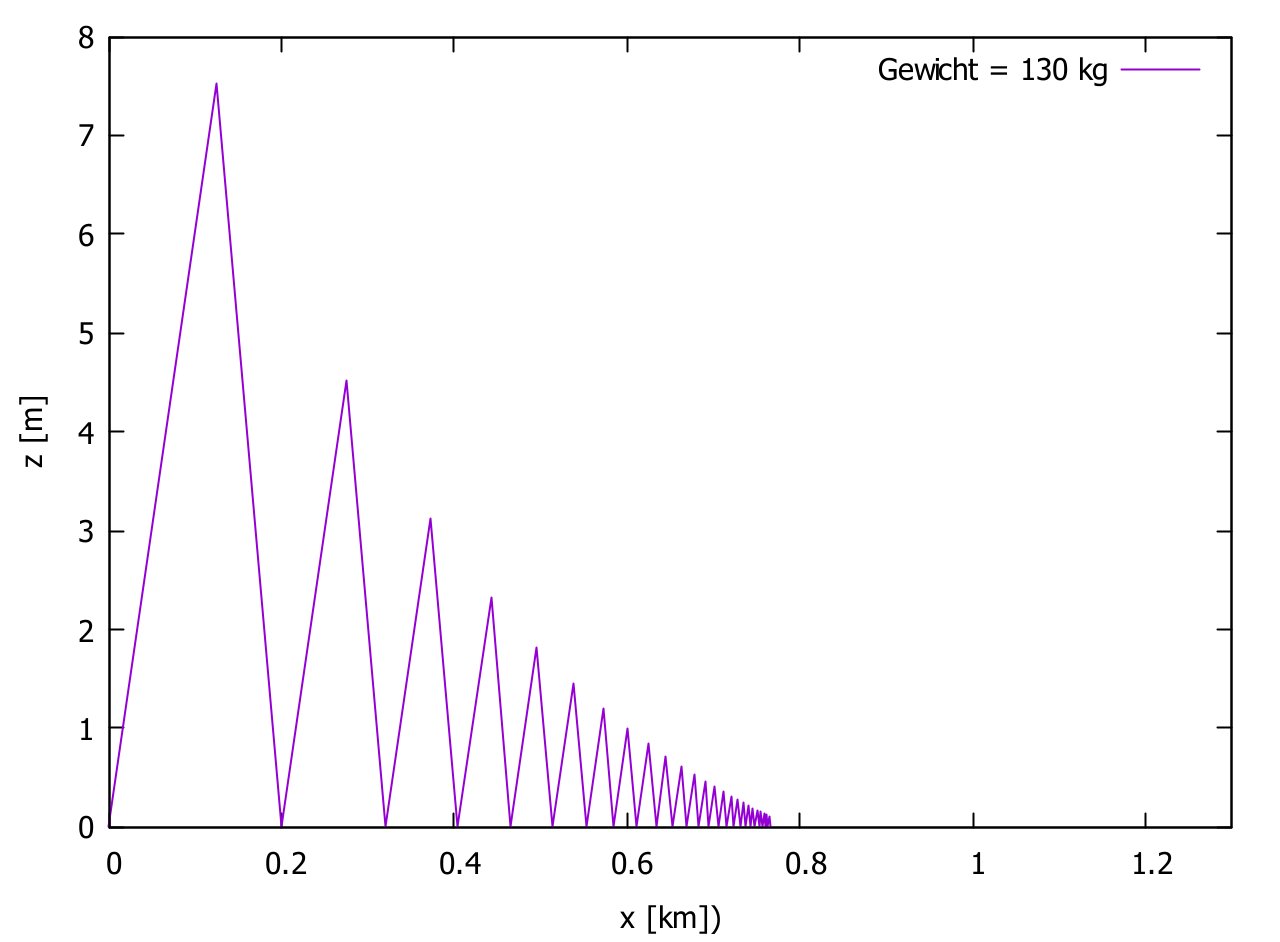
Doch was passiert, wenn die Rampe an der Stelle s_max nicht mehr fällt, sondern steigt oder eben ausläuft? Auch für diesen Fall bekommen Sie die (hoffentlich) richtige Antwort. Voraussetzung: Sie tun weiterhin nichts, die Pedale ruhen. Sie profitieren vom Schwung, den Ihnen die Abfahrt mitgegeben hat: Wo und wann die Kräfte entgegen der Fahrtrichtung die Fahrt beenden werden, sagt Ihnen mein Programm.
Wie üblich, sind die Felder im Programm vorbelegt; Sie geben Ihre Werte ein und klicken auf "los". Nachdem die Ergebnisse in Windeseile auf dem Bildschirm angezeigt sind, können Sie andere Eingaben machen; um zu sehen, was passiert, wenn Sie sich z.B. zusätzliche 10 kg gönnen oder sich eine steilere Abfahrt zutrauen.
Jetzt also nichts wie los und auf

Rampen-Rechner-Ab geklickt!

Eine Variation des Spiels ist dessen Wiederholung (auch das ist im Fahrrad-Allgemein Artikel beschrieben).
Gehen wir von folgender Konstellation aus. Herren-Fahrrad H tritt gegen Damen-Fahrrad D an. H wiegt m_H = 130 kg, D wiegt m_D = 75 kg. (Rad inklusive Herr bzw. Dame). Roll- und Luftreibung seien der Einfachheit halber für beide gleich. H und D fahren einen Hang hinunter und kommen durch geschickte Manipulation mit gleicher Geschwindigkeit unten (z = 0) an. Von dort es geht ohne Pause (und ohne eigenes Zutun, also stehenden Pedalen) auf schiefer Ebene mit Steigung δ bergauf; anschließend auf schiefer Ebene mit Gefälle α wieder bergab, usw und so fort. Die jeweiligen Umkehrpunkte sind v ≈ 0 und v = v_max, entsprechend z = z_max bzw. z = 0 notiert. Physikalisch wird beim Auf kinetische in potentielle Energie und beim Ab potentielle in kinetische Energie umgesetzt, allerdings unter Verlusten durch Roll- und Luftreibung. Bei Wiederholung des Prozesses konvergieren die Maxima kontinuierlich gegen Null; dann ist der Vorrat an Energie verbraucht. Zur Illustration ein Bild, in dem H oder D, wie's beliebt, bergauf und bergab fährt.

Nun die Preisfrage:
Welches Fahrrad ist länger unterwegs?

Gerechnet wird, wenn Sie auf Rampen-Rechner-Auf-und-Ab klicken!

Wer das Bild dem Zahlenwerk vorzieht, möge auf Rampen-Bild klicken!